Non conosciamo altri astronomi che
abbiano esposto idee simili prima di lui. Peraltro i suoi successori non accettarono
le sue ipotesi, fatto, questo, che non contribuì certo alla sua popolarità.
Secondo Plutarco, Aristarco seguiva
la teoria di Eraclide di Ponto che pensava che la rotazione diurna delle stelle
fisse fosse dovuta alla rotazione della Terra sul suo asse. E di lui parla
Vitruvio (I sec. d.C.), il famoso architetto e ingegnere romano, che lo cita
nel De Architectura in una lista di personaggi cui si devono invenzioni
e risultati di particolare importanza per lo sviluppo delle scienze e della
tecnica.
Matematico
ed astronomo egli occupa tuttavia un posto importante nello sviluppo dell'astronomia
matematica; oltre alle sue teorie, infatti, a lui si deve il primo tentativo
di determinare le dimensioni e le distanze del Sole e della Luna.
I valori da lui ricavati, per quanto
errati, furono utilizzati da tutti i suoi successori per più di 1500
anni. Solo verso il XVII secolo, infatti, dopo le osservazioni di Copernico,
Tycho Brahe, Keplero ed altri si ebbe una determinazione corretta di queste
distanze.
L'unica opera di Aristarco sopravvissuta
si chiama Sulle grandezze e le distanze del Sole e della Luna e fornisce,
fra le altre, la deduzione geometrica della distanza fra la Terra e il Sole
sulla base delle osservazioni, ma non fa alcun cenno alle sue ipotesi eliocentriche.
Le ipotesi da cui parte possono
essere riassunte come segue:
- la Terra è una sfera
- il Sole è lontano, ma
non troppo perché i suoi raggi colpiscano Terra e Luna con angoli
diversi
- la Luna orbita intorno alla Terra
in modo che sia possibile avere le eclissi
Ecco la sua discussione.
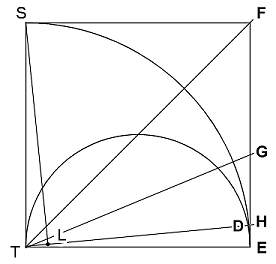
Fig. 1
Nella figura 1 siano: S la posizione
del Sole, T quella della Terra, L quella della Luna quando metà della
sua superficie è illuminata (primo o ultimo quarto).
Dalle osservazioni si ha che l'angolo
(STL) fra Sole e Luna al primo quarto è di 87°, allora TSL = 3°.
Ora sia ETH = TSL = 3°. Costruiamo
poi TG bisettrice dell'angolo FTE (= 45°).
Considerando la
circonferenza con centro in T e raggio = TE, il rapporto fra le lunghezze
dei segmenti GE e HE (tangenti alla circonferenza in E) è maggiore
del rapporto fra gli archi e gli angoli relativi (*). Il
rapporto GE/HE sarà quindi maggiore del rapporto fra ¼ e 1/30 di un
angolo retto (STE), cioè maggiore di 15/2.
Inoltre FG : GE
= TF : TE = v2 (**), maggiore di 7/5, quindi (poiché
FE=FG+GE): FE/GE>12/5.
Combinando le due disuguaglianze
troviamo che FE/HE > 15/2 x 12/5 = 18 e il rapporto ST/TL è uguale,
per similitudine, a TH/HE e questo è a sua volta maggiore di FH/HE.
Quindi ST/TL è maggiore di 18.
Ora, il rapporto
fra due corde disuguali è minore del rapporto fra gli archi sottesi (***), consideriamo quindi DE che sottende un angolo al
centro di 6° sul semicerchio TDE e il lato (uguale al raggio) di un esagono
regolare che sottende un angolo di 60°.
Troviamo che (½ TE)/DE < 10,
quindi ST/TL < 20.
Con l'uso della trigonometria, sconosciuta
ad Aristarco, la sua deduzione è equivalente alla situazione mostrata
in fig. 2
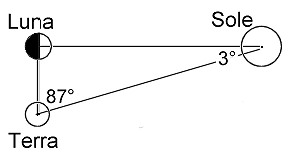
Fig. 2
Il rapporto fra le distanze del
Sole e della Luna è dato da sen 3°; il ragionamento di Aristarco equivale
a calcolare un valore per questa espressione, il cui risultato è:
1/18 < sen 3°
< 1/20
In altri termini il Sole è
18 – 20 volte più lontano della Luna.
La distanza angolare fra Sole e
Luna viene stimata da Aristarco in 87°, il valore corretto è di circa
89° 51' che porta il rapporto fra le due distanze a circa 400 volte. L'errore
deriva dalla difficoltà di misurare esattamente l'angolo formato fra
il Sole e la Luna e dalla difficoltà di calcolare ed osservare il momento
esatto in cui la parte illuminata della Luna è del 50%.
(i valori oggi correntemente usati
sono: distanza media della Luna: 384 400 km, distanza media del Sole: 149
600 000 km, il rapporto fra le due distanze è quindi circa uguale a
389.2).
Stesso valore (18-20 volte) ha il
rapporto fra le dimensioni del Sole e della Luna, visto che essi hanno lo
stesso diametro apparente, come dimostra l'esistenza delle eclissi solari.
Stranamente Aristarco usa il valore
di 2° come diametro angolare del Sole e della Luna. Archimede, però,
cita un valore di 0.5° (in prima approssimazione è il valore oggi accettato),
attribuendolo ad Aristarco. Forse Sulla grandezza e la distanza del Sole
e della Luna è un'opera giovanile e solo più tardi egli
formulò l'ipotesi eliocentrica e calcolò un valore più
accurato delle dimensioni angolari del Sole.
In realtà, come a molti dei
filosofi greci, ad Aristarco non interessava tanto trovare valori accurati,
quanto formulare la teoria e il procedimento per arrivare al risultato.
Procedimento perfettamente valido
e corretto, nonostante i valori errati lo portassero a conclusioni sbagliate.
(*) Dato un angolo alla circonferenza il segmento di tangente è maggiore
dell'arco e della corda sottesa dall'arco: TanA > ArcA >CrdA.
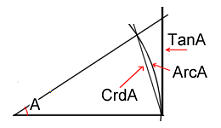
Quindi il teorema cui si riferisce
Aristarco dice che:
TanA : TanB >
ArcA : ArcB > CrdA : CrdB
Espresso in termini moderni, facendo
uso della trigonometria, questo teorema è equivalente all'espressione:
tanA/tanB > A/B
> senA/senB
(per 0° < B < A < 90° con
A e B espressi in radianti).
(**) In un triangolo qualunque, la bisettrice di un angolo divide il lato opposto
in due segmenti proporzionali ai lati adiacenti (v. Legendre: Elementi di
Geometria Piana, libro III, prop. XVII, pag. 88). Caso particolare di questo
teorema è quello del triangolo isoscele, in cui la bisettrice dell'angolo
al vertice divide il lato opposto in due segmenti uguali.
(***) Tolomeo (Almagesto I,10), dimostra che in una circonferenza, date due corde
disuguali CrdA e CrdB che sottendono gli archi ArcA e ArcB, se CrdA > CrdB,
allora il rapporto fra le due corde è minore del rapporto fra gli archi:
CrdA : CrdB <
ArcA : ArcB.
