I limiti fisici della tecnologia
   Rodolfo Baggio

Alcune delle leggi ed espressioni fondamentali con le quali è possibile stimare un limite fisico per la tecnologia di vari elementi di un sistema informatico.

Legge di Boltzmann 

In un un gas ideale: 

PV = nRT

 il prodotto pressione · volume è proporzionale alla temperatura del gas, quindi all'energia cinetica media delle sue molecole: 

P = N<1/2mv²> = 2/3N<1/2mv²>

Ora: N/n = num. molecole/mole = N_A (numero di Avogadro) = 6.02·10²³  mole^-1, R (costante molare di Rydberg) = 8.314 J/mole allora:

<1/2mv²>  = <E> = (R/N_A)·T =  k_B·T

k_B  è la costante di Boltzmann = 1.38·10^-23 JK^-1, costante di proporzionalità fra l'energia cinetica molecolare e la temperatura.
In altri termini, la temperatura è una misura dell'energia cinetica media di un atomo (o molecola).

Entropia

L'entropia in sistema isolato diminuisce e tende verso il massimo quando il sistema è in stato di equilibrio termodinamico (seconda legge della termodinamica).
L'entropia S è proporzionale all'energia E del sistema, per piccole variazioni di S:

temperatura T = ¶E/¶S

Quantitativamente l'entropia vale ln(N) dove N è il numero di stati possibili. In un sistema binario (in logica booleana),  S = ln2, quindi

E µ ST = k_B·T· ln2                  (f.1)

Per calcolare un limite al flusso di informazioni calcoliamo la potenza dissipata per trasmettere  n bit a distanza d alla velocità c (velocità della luce). Sarà:

P = n·k_B·T  (d/c)  n²                (f.2)

dove:  P = potenza (W), k_B = costante di Boltzmann = 1.38·10^-23 JK^-1, T = temperatura (°K), d = distanza di trasmissione (m), c = velocità della luce = 2.998·10⁸ m/s, n = frequenza operativa (Hz), n = numero di operazioni parallele.

Limite fisico alla potenza di calcolo

Supponiamo di avere un computer che dissipi 1 W a temperatura ambiente, allora (vedi f.1):

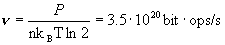
Se il volume è di 1 cm³, sempre dissipando 1 W, allora (f.2):

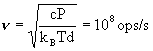
Convertito in mips questo è l'equivalente di 10⁸ – 10⁹ pentium.

Frequenza di Larmor

In un campo magnetico B, un elettrone in moto orbitale intorno al nucleo varia la sua frequenza angolare di una quantità:

Dw = ± e / 2m_e·B

detta frequenza di Larmor.
In altri termini: se si uguaglia la forza di Lorentz a quella centripeta, il raggio del moto circolare di un elettrone, detto raggio di Larmor, è dato da:

R = m·v /(e/B)

il numero di orbite in un secondo, la frequenza di Larmor vale:

f₀ = e·B/2p·m_e

con:  m_e = 0.9·10^-30 kg , e = 1.6·10^-19 C ® e/2m_e =  8.89·10¹⁰  quindi, f₀ » GHz.

Limite alla densità di registrazione su memorie magnetiche

Il limite dipende da molti fattori: il materiale magnetico, la velocità di rotazione del disco, l'altezza di volo della testina, ecc.
Un fenomeno importante è il superparamagnetismo. A volumi inferiori ad un valore critico (v_c), la magnetizzazione fluttua statisticamente per motivi termici

v_c = ln(2t·f₀) k_B·T/K_u

dove f₀ = frequenza di Larmor ~ 10⁹ Hz.
Per assicurare una stabilità di t = 100 anni:

K_u·v_c / k_B·T ~ 43

K_{u è una costante caratteristica del materiale.
Per i materiali noti oggi,} la densità critica è di: 40 - 50 Gb/in²  (le densità raggiunte oggi sono di ~10 Gb/in²)

Teorema di Shannon

Il teorema dà un limite superiore alla capacità di un canale trasmissivo in bit per secondo (bps), come funzione della banda disponibile e del rapporto segnale / rumore (S/N) del canale. Il teorema si può esprimere come:

C = Df · log₂(1+ S/N)

dove C è la capacità del canale e Df  la larghezza di banda, S la potenza media del segnale, N la potenza media del rumore.
Il rapporto S/N è di solito espresso in decibel (dB) = 10 · log₁₀(S/N), così, per esempio, un rapporto S/N di 1000 è comunemente espresso come 10 · log₁₀(1000) = 30 dB.

Come curiosità ecco alcuni valori di "larghezze di banda" legati a parti del corpo umano considerate come canale di trasferimento di informazioni:

• cervello > 10 Gbps
• occhi  » 10 Mbps
• pelle  »  1 Mbps
• orecchie e naso  »  100 kbps
• gusto  »  1 kbps

Limite alla larghezza di banda

Su una fibra ottica si ha trasmissione ottimale in tre bande di ~ 200 nm (10^-9 m) centrate a 0.85, 1.3 e 1.5 mm.
Poiché Df = c_mDl / l², (con l  = 1.5 mm c_m = 66% c):

f ~ 20·10¹² Hz ~ 20 THz (~Tbps)

Dal teorema di Shannon (canale gaussiano e S/N=10), poi:

C = Df·log₂(1+S/N) = 3.45 Df µ Tbps