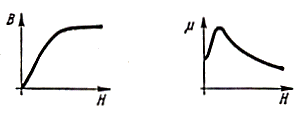ntroduction to Digital Magnetic Recording

   Rodolfo Baggio
   IBM Customer Executives Briefing Center
   Mainz, Germany, October, 1986

Table of contents

1 - Introduction
2 - Principles of magnetics
3 - Digital magnetic recording

• Magnetic materials
• Writing
• Reading
• Pulse superposition

4 - Conclusion
5 - Bibliography

---

1 - Introduction

The search for ways to store information on an external device at higher densities, and for retrieving it with higher speeds is one of the most important challenges of research in computer science.

Storage devices are complex and their design involves the knowledge of many different technologies, from magnetics to electronics, from chemistry to aerodynamics.

The basic technology for the most used storage device is digital magnetic recording. This is a special application of the magnetic recording technology which was originally developed to record and reproduce sound. In this case, the main requirement is to have a good similitude between the input and output of a continuous waveform signal, therefore the frequency response characteristics are the major concern of a designer of such systems.

In a digital storage device, the major concerns are (besides the cost):

• density of information (number of bits in a unit length, usually measured in bits per inch and tracks per inch)
• access time (the time needed to position the read and write mechanism in a given position)
• data transfer rate (number of bits transferred in a unit of time)

The most important of these parameters is the density due to the influence it has on the others. For example, data transfer is directly proportional to linear density while access time (seek time) is inversely proportional to track density.

Magnetic recording is based on the interaction between a magnetic storage medium and a magnetic transducer in relative motion with respect to one another. The relative motion is usually obtained by moving the medium.

The magnetic field generated by the transducer (head), a small electromagnet, magnetises in a permanent way a small region of the material. By changing the direction of the current in the coil of the electromagnet, it is possible to generate two different directions in the magnetic field induced on the surface. These two different states are what we need to "write" two different bits.

Conversely, when one of the tiny magnetised regions passes under the head, an electrical pulse is induced in the coil of the electromagnet. The pulse detected is proportional to the rate of change of the magnetic flux and the direction of the current depends on the direction of magnetisation in the region of the surface. In this way it is possible to "read" back the different magnetic states written on the storage medium and to interpret them as different bits.

In the so called longitudinal recording, the principal direction of magnetisation is in the plane of the surface, parallel to the direction of the motion. The path generated by the transducer on the surface, also parallel to the direction of motion, is called a track.

The following characteristics of the materials involved are of major importance to magnetic recording:

• the storage layer must be capable of retaining in a stable way a sequence of permanent magnetic states
• the recorded pattern can be modified only by erasing or rewriting (changing the magnetised state)
• the head is a device that has the basic functions of providing a confined and intense magnetic field in order to magnetise a small region of the material (writing process) and of producing a detectable electrical pulse when passing by a magnetic flux arising from a magnetised state of the storage medium (reading process).

Therefore, the recording surface is made of a high permeability magnetic material, i.e. it is able to have a good "response" to a magnetic field, and the head is an electromagnet, made with a coil winding and a magnetic core with a gap.

In order to achieve high recording densities, it is necessary to write a binary bit in the smallest possible space, and to place the bits as close as possible. To be successful in this, the interactions and the relationships between head and surface are extremely important. Since it is not possible to focus magnetic fields like light, the only possibility to produce intense and confined magnetic fields and to record dense bits, is to have narrower gaps in the electromagnet, smaller spacings between head and medium, thinner layers and higher speed of relative motion. In addition to that, narrower pole tips will determine higher track density.

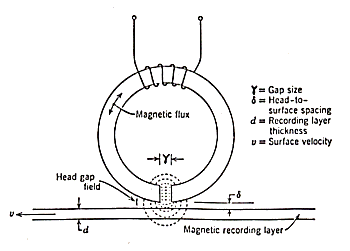
Fig. 1.1

The good balance of these parameters (shown in fig. 1.1) is the most important and delicate task for the success of the whole process.

In magnetic recording, the writing process is not, as one might think, the most critical.

As a matter of fact it is possible to write bits at higher density than they can be read and converted into a detectable signal by appropriate electronics.

Writing is done by the trailing edge of the magnetic field generated by the head. For reading the entire magnetic field of the stored bit is used to induce an electrical pulse in the reading head, and this pulse must be able to give a large signal to noise voltage in order to be easily and clearly converted into a digital form.

The main limiting factor is the distortion of the signal produced by the closely packed bits. If the packing factor is too high (bit crowding), the magnetic field detected is the overlap of the fields from the adjacent bits. The total field sensed by the reading head gives, in this case, an induced signal with a shape different from that produced by a single bit, thus leading to the impossibility to interpret the recorded pattern in a correct way.

2 - Principles of magnetics

It may be useful to recall some of the concepts of magnetics. In this part the concepts and the relationships are reviewed, the more important to understand the digital recording processes well.

The interactions between electric currents and magnetic forces were discovered and explained in the first half of 17th century. From these researches it was found that a piece of magnetic material experiences a force when it is put in a region in which there is a presence of an electrical current. In this region a magnetic field is generated by the current. If the conductor is linear, of infinite length and the current flowing has intensity i, the value of the magnetic field B is given by:

B = k i / r

where r is the distance from the conductor.

In the CGS system of units, B is measured in Gauss.

In other words, the field B is proportional (k is a constant of proportionality) to the intensity of the current and is inversely proportional to the distance. If we have a circular turn of radius R, the field, in the space external to the loop, at a distance r, is:

B = k i a / ( r² + R²)^3/2

(a = area of the loop).

For an infinite linear coil (solenoid), made of N turns, the field in a point internal to the solenoid, has the value:

B = k 4p N i

if the coil is circular (toroid):

B = k N i / r

r is the toroid internal radius.

All of these examples show that the magnetic field, due to an electrical current, depends only on the intensity of the current and on some geometrical characteristic of the circuit.

Since it is not possible to "see" a field of forces, whatever they are, magnetic, gravitational, electrical etc., we use a graphical representation for it. We draw the so called field lines, these lines represent the trajectories of a particle or a piece of material that experiences the forces of the field. The force is always tangent to the lines, their density is proportional to the strength of the field.

The similarity between magnetic fields generated by currents and by magnetic materials may be seen in fig. 2.1, where the field lines are drawn for a magnetic needle and a solenoid.

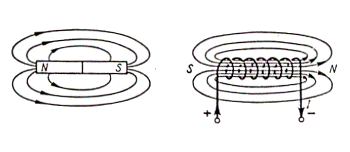
Fig. 2.1

If a current produces a magnetic field, we should expect that a magnetic field is able, in some way, to give rise to an electrical current.

We can define the flux F of B on a surface s as the product between these two quantities:

F = B s

The basic relation, known as Faraday's law, linking B to an electrical current is:

E = k D F / D t

i.e. any variation in time of a magnetic flux, produces a voltage pulse. This relation may also be written as :

E = k v D F / D x

that means that a pulse is also produced in a conductor every time there is a moving magnetic field (with speed v).

This is the principle on which a dynamo works. A conductor, usually a coil, is moved with a certain speed in a region where a magnetic field exists.

Let us take a coil, and put a piece of material inside. The field outside is described by the equations above, but what is about the magnetic field inside the material? In this case the magnetic field generated by the current flowing in the coil will interact with the electronic currents inside the material, as a result we shall find some difference in the magnetic field inside. For historical reasons the field due to a magnetic material has a different name, this one, the field H, is related to B by:

B = m H

H is measured in Oersted, the quantity m is called magnetic permeability, in vacuum (or in air) m = 1 , so no difference exists in this case, B and H have the same behaviour. In any other material m is a complex function and it depends on the material and on the field applied to it. The difference between the fields B and H inside a piece of magnetically active material is shown in Fig. 2.2.

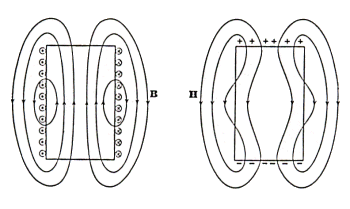
Fig. 2.2

From a physical point of view, the permeability of a magnetic material is similar to the conductivity of an electric conductor, the higher it is, the bigger will be the magnetic properties of the material. Substances for which m ~ 1 show very small or no magnetic properties, they are called amagnetic materials.

Usually, the permeability, for a specific material, is given related to the permeability of vacuum. Being a ratio, m (r) (relative permeability), is a pure number.

If m is close to 1 (the magnetic properties of the material are not too big) we call these substances paramagnetic if m > 1, diamagnetic if m < 1.

From a magnetic point of view, a material is interesting only if it has good properties, this is the case of the ferromagnetic materials, in which m >> 1.

Since the permeability is not a constant, in a ferromagnetic material the relation between B and H is not a linear relation. Figure 2.3 shows this relation, the curve is known as hysteresis loop.

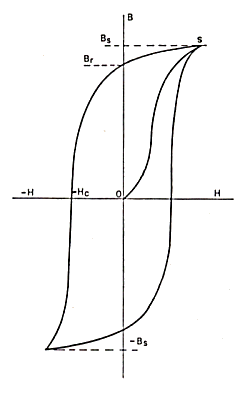
Fig. 2.3

Let us consider a piece of ferromagnetic material wound with a coil.

At the beginning H = 0 and B = 0. Increasing H (increasing the current in the coil), B increases in the way shown by the curve O-S up to a value Bs, this is called saturation value, i.e. from now on, even big increases in H will result only in insignificant increases in B. The material is fully magnetised. If now H is decreased, B decreases along the curve S-Br. The important thing is that when H reaches 0, B is not zero, but has the value Br (residual magnetisation). This means that the material preserves now a magnetisation even in absence of an external field, if there are no external interferences, the magnetisation is permanent. In order to annul the field B, we must apply a negative field -Hc, called coercive field, inverting the current in the coil. The negative part of the loop is symmetrical to the positive one.

The behaviour of permeability is shown in fig. 2.4. Its value is related to the slope of the hysteresis curve, while H is increasing, m goes from an initial value to a maximum and then decreases when the B-H curve flattens.

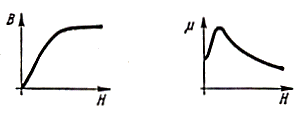
Fig. 2.4

It took a long time before a fully understanding of this phenomenon was reached. We may now think of a ferromagnetic substance as composed of small domains. In normal conditions, in the absence of external field these domains are randomly oriented, so that on the average the total magnetisation is zero. An external field H will produce a progressive orientation of the domains along the field direction as long as its intensity is increasing. A saturation will occur when all the domains are aligned with H. To destroy this alignment we need a magnetic field with an opposite direction, and an intermediate intensity between zero and the saturation value.

The coercivity (the value of the coercive field) is an important physical parameter, it represents the "inertia" that a ferromagnetic substance has, with regards to a magnetic field. A low coercivity means that the material's magnetisation can easily be changed. Low coercivity materials are often called soft magnetic materials, high coercivity are called hard materials. The hysteresis loops in these two cases are shown in Fig. 2.5.

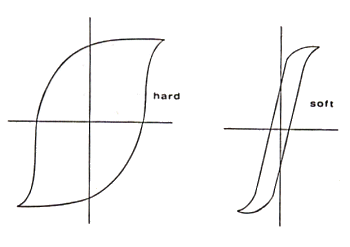
Fig. 2.5

When different materials are present, the magnetic flux tends to confine itself in a high permeability path, in the same way that an electrical current tends to flow in a high conductivity path. Given this analogy, we may speak of magnetic circuits as well as of electrical circuits. An example is shown in Fig. 2.6, along with its electrical equivalent.

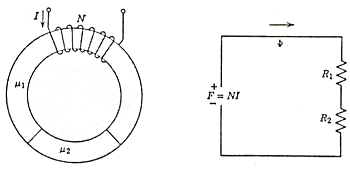
Fig. 2.6

The magnetic flux linking the circuit is:

F = B s

where s is the cross sectional area of the toroid.

If m ₁ and m ₂ are large, the flux will "flow" in the toroid, along it. Since the lines of flux are continuous:

B₁ = B₂ or m ₁H₁ = m ₂H₂

We also have (see the expression above for the field of a toroid):

H₁ l₁ + H₂ l₂ = N i

where l₁ and l₂ are the length of the materials with m ₁ and m ₂ , N is the number of turns and i is the current flowing in the coil.

We can define a magnetomotive force F = N i, and a reluctance R = F / F

That is R = H l / B s , or R = l / m s (since: B = m H) , with a perfect analogy with the definition of the resistance: R = l / s s (s is the specific conductivity). Thus we have in the magnetic circuit:

F = F₁ + F₂ = (R₁ + R₂) F

To complete the analogy, F, which is measured in ampere-turns, may be interpreted as a voltage source, or electromotive force.

If one of the materials is air, i.e. there is a gap in the toroid, whose permeability is one, the total reluctance of the circuit is ( m (air) = 1):

R = (l₁ / m ₁ s) + (l₂ / s)

The reluctance depends only on the geometrical dimensions of the gap. The magnetic field is divided in the circuit according to the reluctances of the various parts, since m ₁ >> 1 (ferromagnetic

material), H will tend to "concentrate" itself in the low permeability portion of the circuit, and to "expand" outside the air gap. If the gap is filled with an amagnetic but conducting material, electronic currents will arise in it as consequence of a magnetic flux variation. These currents will give rise to a magnetic field that will reinforce the tendency to expand out of the gap (Fig. 2.7).

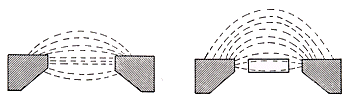
Fig. 2.7

3 - Digital magnetic recording

In theory it is possible to fully explain the behaviour and the characteristics of a digital device from the principles and the formulas we have seen in the previous chapter. Practically this task is quite impossible. We introduced a lot of simplifications and, in order to understand the main concepts, we made many assumptions that are not to be found in the real physical world. The real world, especially when dealing with magnetic and electric phenomena, is very complex. Magnetic properties are highly non linear and many different parameters affect the magnetic behaviour in several ways. Our main objective is to understand and to explain the basic concepts of digital magnetic recording. To do so we still need to make some approximations and to introduce restrictive hypotheses, but we also need to introduce some new parameters and to examine, at least from a conceptual point of view, their mutual interactions.

The basic situation we want to describe is shown in figure 3.1.

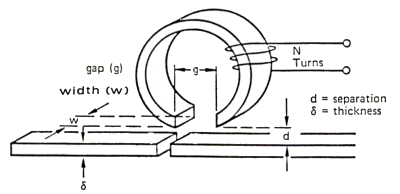
Fig. 3.1

 

Magnetic materials

Before examining this situation, let us say a few words about the materials used in a storage device. From the considerations made in the introduction on the principles of operation of magnetic recording and from the fundamentals of the magnetic theory we are able to better specify the main characteristics of the ideal materials we should need.

We have seen that the small electromagnet that forms a read/write head must be able to produce a very intense and spatially well confined magnetic field. In order to write densely packed bits, it must be possible to change the direction of this field with a high frequency. In other words, we should succeed in inverting the magnetisation of the head in a very short period of time.

With these requirements we are describing a "soft" magnetic material, with high relative permeability and high saturation magnetisation. Moreover, the need for high frequency inversions in magnetisation may be stated as a request for low coercivity and relatively low residual magnetisation (remanence). Table 3.1 gives the values for some of the materials matching these characteristics.

Table 3.1

 

On the other hand, the medium on which we record data must be able to retain permanently the information stored at high density. That is to say that we need a ferromagnetic material with high permeability in which the magnetic domains are very small in order to be able to magnetise tiny regions with different orientation. This is usually obtained by coating a non magnetic substrate (usually aluminium) with a mixture made of an inert material used as a binder (for example epoxy resins), in which are imbedded small particles of the ferromagnetic substance. The magnetisation is preserved, in absence of external forces, if the material has high coercivity and high remanence. Finally, if the saturation field is not too high, i.e. it is relatively "easy" to magnetise the material, we have the ideal medium to record information. Table 3.2 gives the characteristical values for some of the materials currently used.

Table 3.2

 

It is worth noting that all the values given in the tables above are average and indicative only. The actual values depend on the mechanical and thermal treatments the material receives during the fabrication. For a coating substance, for example, the magnetic properties depend on the size and the shape of the particles used, on their density and on their orientation on the surface, on the methods used to finish the surface etc. There is no theory able to predict the influence of all of these parameters, only direct measurements after different trials may show which result is the best.

Writing

Let us now examine the two fundamental processes of digital magnetic recording: writing and reading. The best way to understand a physical phenomenon would be to have an analytical expression that describes it. In other words, a formula in which all of the parameters of interest for some process are contained, and the mathematical relations among them are completely defined, would allow us to explain in a simple way, no matter how complex the formula is, every possible behaviour and dependency of the parameters of the process we are investigating. In the case of the writing of magnetic information, we are facing a magnetic field generated by an electromagnet, made with certain materials, having certain geometrical, electrical and magnetic properties. Therefore we are looking for an expression relating quantities like geometry of the head, number of turns in the coil, flying height, current intensity etc. to give the intensity of the field produced and its form in the space outside the head. Unfortunately this expression does not exist.

We need to introduce simplifications and approximations to derive a meaningful relation, and, usually, the validity of such expressions is proportional to the number and the type of hypotheses we make. The type of hypotheses is defined by the objective we have in deriving the formula.

In the present instance, we are mainly interested in understanding the role played by the several quantities, and in being able to predict, at least roughly, how the resulting field is affected by changing one or more of those parameters.

A useful description of this kind was given by O. Karlquist. The approximations introduced are the following: the head (fig. 3.2) has infinite length, with a gap of width g and the pole faces are parallel to the recording medium. The relative permeability of the core is infinite and the field produced is uniform across the gap. The latter is the major departure from the real case (also shown in fig. 3.2), but it is a good approximation for small gaps and for distances up to about g/3, that is a situation close to the real case.

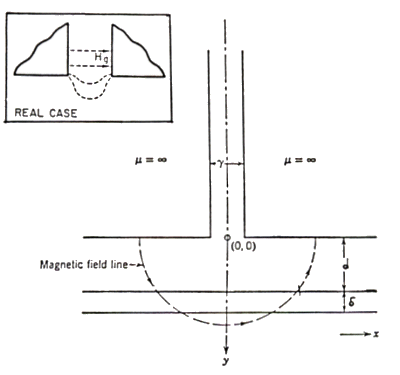
Fig. 3.2

The expression that gives the field H generated by such head in the point (0,0) (in the gap) is:

Hg = N i / g

If we want to evaluate a real case, we need to introduce a quantity called head write efficiency a _w. This is defined as the ratio between the total magnetomotive force (the product N i) of the head and that of the coil. It is assumed that an air gap may lead to some losses.

The value for a _w is:

a _w = N i - D N i / N i = 1 - D N i / N i

The field is then:

Hg = 4p a _w 10^-3 N i / g (Oe)

with i in Amp and g in meters (in the next part we shall define a read efficiency as well, which is easier to calculate for practical purposes).

The field lines for H (fig 3.2), since it is uniform and given the geometry of the configuration, are semicircles with the center in the point (0,0). The expression for the intensity of the field in any other point below the gap is more complex and is given in graphical form in fig. 3.3, splitting the components of H along the x and y axes.

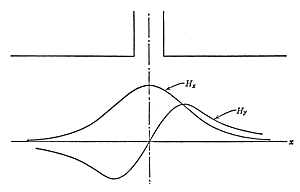
Fig. 3.3

It is possible to derive a simple relation for the field intensity on the points on the axis of the gap, at distance y from it:

H(0,y) = 2 Hg / p tan^-1 (g/2y)

At the bottom of the coating the distance is the sum of the flying height (separation d) and the coating thickness (d ), y = d + d , in this point H has the value:

H(0,d+d ) = 2 Hg / p tan^-1 (g/2(d+d ))

Figure 3.4 shows the variations for different distances from the gap.

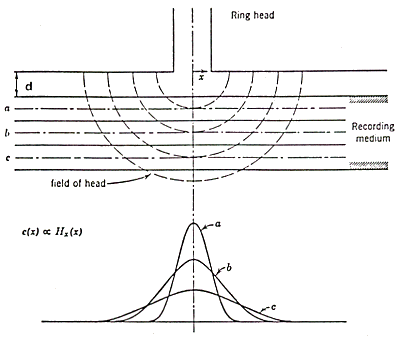
Fig. 3.4

From the discussion in chapter 2 we may derive that there is a reciprocity between a current and a magnetic field. We have seen that a coil in which a current flows produces a magnetic field, and that a moving magnetic field is able to produce a current in a coil. If the permeability of the core is very high, it is a valid approximation to state that the relative permeability is infinite. Under these conditions we may think of the head as a linear element, in which a current pulse is proportional to the field that generated it. We can apply this "principle of reciprocity" in order to better understand the behaviour of the parameters and their relations. For example, what fig. 3.4 really shows is the shape of an electrical pulse e(t) produced across the coil. For the principle of reciprocity, since e(t) is proportional to H, we can think that the intensity of the magnetic field has a similar shape.

It is important noting that H has a strong dependence on the distance, even for small increases. Moreover, the pulse shape broadens, while the intensity is decreasing. This means that without corrections, i.e. increasing the current to give a stronger field, we have writing density limitations if we raise the separation of the head from the medium or the thickness of the coating.

Reading

The reading process is fundamentally ruled by Faraday's law. For a coil made of N turns the electrical pulse induced is:

e(t) = - N D F / D t = - N v D F / D x

e(t) is a function of time and it depends on the variation of the magnetic flux. This variation may be expressed in terms of the spatial distribution of the magnetization in the medium and of the relative velocity v between the medium itself and the head. This means that to be able to read we must detect the changes in magnetization generated in the medium. The shape of the pulse, its time dependency, is defined by the spatial distribution of the magnetic field (fig. 3.5).

Fig. 3.5

The pulse will have a maximum in correspondence with the change in magnetization at the border of a "bit" (the flux change is maximum here), it will then decrease to a zero value while the magnetization becomes uniform (one more approximation) in the rest of the magnetised region.

In the real world several factors, dependent on the geometry of the configuration and on the materials, affect the pulse. First of all a head has finite dimensions, this fact may be reflected in introducing an efficiency factor a _r. The read efficiency is defined in terms of the reluctances of the parts composing the magnetic circuit of the head:

a _r = R_gap / (R_gap + R_core)

From the definition of reluctance R = l / m s, if s_c and s_g are the cross sectional areas of the gap and the core, and g and lc their length:

a r = (g/s_g) / [(l_c/s_c m _c) + (g/s_g)] = 1 / [1 + (l_c s_g / g s_c m _c)]

where m _c is the permeability of the core and m (gap) = m (air) = 1.

If the head has uniform cross sectional area, or the difference between s_c and s_g is not too big (usually a good approximation):

a _r = g / (g + l_c / m _c)

When the head is not completely saturated (this is usually the case since complete saturation is only a mathematical abstraction) we may assume that the read and write efficiencies have about the same value.

In order to describe the detected pulse, we now need to evaluate the factor D F / D x.

In the ideal case we have a sudden and sharp inversion of magnetic field between two adjacent zones. In the real physical world such clear changes do not exist, we shall experience a continuous transition that will take some small but non zero space to happen. A good approximation is to think of a series of alternating bits as having a sinusoidal change in magnetization, i.e.:

B(x) = B_r sin (2p x / l )

where Br is the remanence of the material, and l is the wavelength of the recording pattern, i.e. the linear dimensions of the bits along the track.

The expression for the pulse e(t) can be derived mathematically from these assumptions and, in the early 50's, the dependencies of e(t) on the geometrical parameters were confirmed experimentally. The relations are:

Thickness factor:

T(l ) = 1 - exp (- 2p d /l )

Separation factor:

S(l ) = exp (- 2p d/l )

Gap length factor:

G(l ) = [sin (p g/l ) / p gl ]

where d is the thickness of the medium, d the distance between head and medium (flying height) and g the gap length.

A better approximation for G(l ) is obtained by multiplying it by the quantity:

[5-4(l /g)² / 4-4(l /g)²]

It was also found that these factors are independent. This means, for example, that if we vary the flying height d, having fixed all of the other variables, the value for e(t) will change according to the expression S(l ). Thus the expression for the pulse induced is:

e(t) = 10^-8 N W a _r (m / m +1) v B_r T(l ) S(l ) G(l ) cos(2p vt/l )

where :

For constant velocity, as a function of frequency (f = v/l ) the peak output would follow a curve like in fig. 3.6.

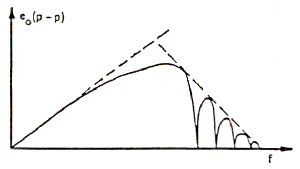
Fig. 3.6

At very low frequencies (low rate of flux change) the amplitude of the pulse is smoothly increasing. After having reached a maximum, depending on all the parameters seen above, the peak output has a marked decrease, mainly due to the separation factor and to the gap length factor, if it is very long with respect to the spacing.

The sinusoidal change in magnetization, as stated before, is an approximation. A better representation is given by the so called arctangent transition. The magnetic field is supposed to change according the law:

B(x) = - (2 B_r / p ) tan^-1(x/a)

This type of transition is shown in fig. 3.7.

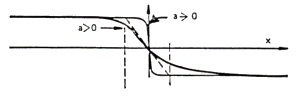
Fig. 3.7

The quantity a is the slope of the curve in the region of the change, its value depends on the magnetic characteristics of the medium and on its thickness:

a = B_r d / 2p H_c

(H_c is the coercivity of the medium).

It can be noted that the ideal step transition is a special case of an arctangent transition (when a = 0).

The expression for e(t) that can be derived is, obviously, more complex. However, the sinusoidal approximation gives a very good agreement with the experimental measurements. Moreover, if the recorded density is very high, the sinusoidal expression becomes again a valid approximation of the real situation (perhaps better than the arctangent).

We can suppose that the pulse induced in the coil has a bell shape (fig. 3.8). If this is true, we need two parameters to define completely the curve: the maximum amplitude (the expression given above for e(t)) and its half height width. The latter may be calculated and has the value:

PW50 = (g² + 4(d+a) (d+a+d ))^1/2

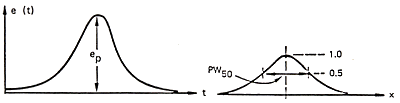
Fig. 3.8

This value depends only, with the exception of a, on geometrical parameters. It may be seen as a measure of the resolution of the system.

We are now able to understand the effects of the variation of any parameter on the amplitude and on the "width" of the pulse across the coil. Since, as we saw, the effects are independent, at least to a first approximation, we may examine them separately. Figure 3.9 shows the effect of a spacing (flying height) variation.

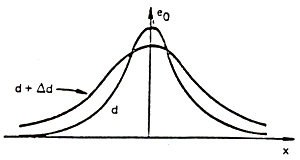
Fig. 3.9

By increasing the spacing, the amplitude of the signal decreases and the pulse broadens and we get worse resolution. Since d and a appear together in the expression for PW50, the same effects happen for variations in a, i.e. for variations in the magnetic characteristics of the medium.

For small changes in the thickness of the magnetic coating, the amplitude increases and the pulse broadens (fig. 3.10). This, like any other broadening of the pulse, is a loss of resolution, or a need for a decrease in the recording density.

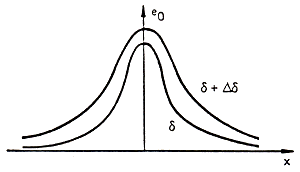
Fig. 3.10

The gap variations are more complicated. Ignoring the efficiency of the head, the amplitude depends on g as shown in fig. 3.11.

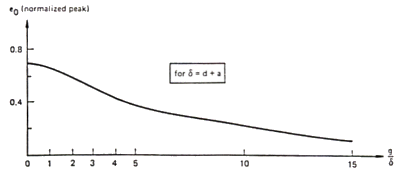
Fig. 3.11

If we introduce the parameter a (efficiency), we should remember that it is a function of g.

In some cases, for particular geometries, the pulse may increase in value over some range of dimensions before decreasing. In any case the pulse broadens with increasing the gap (fig. 3.12).

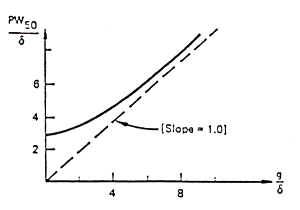
Fig. 3.12

Variations in any other quantity, such as number of turns, head width, velocity, produce changes in amplitude only.

Some of these variations may have different effects. Let us make an example. One might conclude that, in order to increase the peak value for the pulse, it is possible to increase the number of turns in the coil (e(t) depends linearly on this quantity). Now, a series of quickly alternating pulses may be seen as an alternating current and since the materials with which a head is made are usually good conductors, we can see the head as an electrical circuit in which an alternating current is flowing. Thus, we can apply the laws that rule these kind of circuits. The intensity of current will be given by:

I(t) = I₀ exp (- (R/L) t)

where R is the resistance and L the inductance of the circuit.

The main effect of the inductance is to produce a time delay on the current. The quantity L/R is called time constant of the circuit. A time of about 5 (L/R) is needed before reaching 99% of the current. The inductive part of the circuit we are considering is the coil encircling the head core. The inductance of a coil is mainly due to its geometrical characteristics: length of the coil, number of turns, dimensions of the wire, diameter of the coil, spacing between the turns. This means that changing the physical parameters of a coil, we change its inductance, this change is reflected in a variation of the time constant of the circuit and in a variation of the delay with which the current will reach its maximum. If we introduce a delay in the current, we delay the magnetic field produced as well. This will be reflected in a lower magnetization of the medium, or in an increase of the linear dimensions of the bit cell, thus affecting the detected pulse.

Pulse superposition

All the considerations made so far were made taking into account a single, isolated pulse. What we really have is a series of magnetic transitions that appear, after having read them, as an alternating series of positive and negative pulses. The basic phenomenon we should investigate is the composition, and the reciprocal interferences, of a pattern formed by this series of transitions.

If the readback process is, at first approximation, a linear process, we may sum algebraically the head response of every single transition of the series. The total response will depend on the distance between the isolated pulses (bit spacing). In fig. 3.13 is shown the result of the composition of two adjacent saturation reversals.

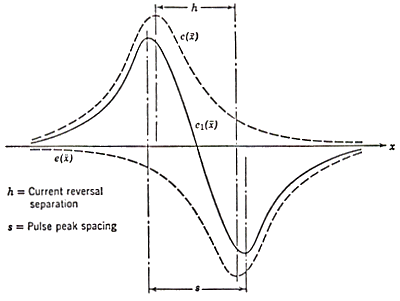
Fig. 3.13

The important effect of this linear composition is that the resulting pattern has a decrease in the peak amplitude and a shift of the peak position. The output amplitude approaches zero as the bit separation h becomes very small. With four reversals the resultant configuration is depicted in figure 3.14.

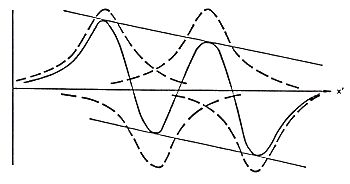
Fig. 3.14

The net result is not only peak decreasing and shift, but also a droop in the shape of the resulting waveform.

The total composition effect is perhaps the most important limiting factor on the maximum bit density that is obtainable from a given configuration. If we sum a long series of pulses, plotting the value for the resultant e(t) vs. the bit density, we obtain figure 3.15.

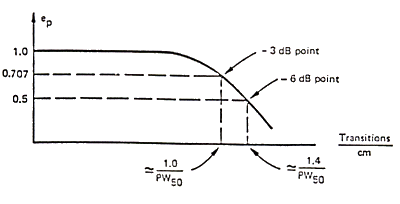
Fig. 3.15

In the figure the points are shown in which the attenuation's of the pulse are 3 and 6 dB. The second one represents a reduction to one half of the peak value of an isolated pulse (e(t) = PW50).

It is important to note, at this point, that we have not mentioned that in any electrical circuit there is an unpredictable noise that may seriously affect the possibility of obtaining a meaningful readback signal.

From a physical point of view, the interferences between adjacent pulses may be seen as interferences between the magnetic fields of the single bits. For a single magnetised region, the head "reads" the field due to that region. Since the dimensions of the bit are finite dimensions, even if small, the field due to an adjacent region will receive a contribution from the previous one. The resulting field read will be, therefore, different from that due to a single bit. Its intensity, if the bits are opposite, will be lower and its modified shape will displace the point of maximum flux change thus leading to a modification in amplitude and shape of the detected pulse.

4 - Conclusion

In a commercial storage device we are interested in having high capacity and good performance. We have seen that the density is the main parameter we must deal with for its influence on performance. It is possible, with the formulas and the approximations given, to find the theoretical limit for the density of flux reversals in a storage medium. The main limiting parameter, from a theoretical point of view, is a self demagnetisation factor that arises when the bit spacing is too small. In other words, the magnetic interference between adjacent bits may be so high that it becomes impossible to recognise the single magnetic transitions. It may be shown that the limit for the linear length (in cm) of a magnetic transition is given by:

l = B_r d / 2 H_c

where d is the medium thickness (cm), B_r is the remanence of the medium (Gauss) and H_c its coercivity (Oersted). For a given material, the density limit is depending on its magnetic properties and on the coating thickness. The theoretical limit for known materials and for known, even if by now not yet achieved, techniques is of the order of magnitude of 10¹⁰ bits per square inch.

The relations given and the considerations made may help us in better understanding the properties and the behaviour of a storage device. They may also let us understand some of the reasons behind certain choices or technical solutions adopted in a machine. For example, let us consider a magnetic disk. A head is usually flying over a spinning disk sustained by the air flow generated by the moving surface. The head disk separation will not be constant across the radius of the disk. In fact, assuming constant rotational speed, on an outer diameter the linear velocity is higher than on an inner diameter. Thus we can assume that the air flow generated has higher intensity and the separation increases toward the border of the disk. Now, if the separation increases, the amplitude of the detected current pulse decreases and the pulse itself broadens. On the other hand, the amplitude loss may be compensated by having a higher thickness of the coating on the outer regions of the platter. This fact produces again a pulse broadening. To gain in resolution we must have a higher spacing between the bits.

Therefore we are able to understand that, in order to get a pulse uniform in amplitude and in shape, a magnetic disk would have a variable coating thickness and a constant number of bits per track.

This one and other qualitative conclusions may be derived from the formulas and the considerations made so far. It could be quite impossible to get exact quantitative results for a given set of materials.

Even if we could remove some of the approximations we made and solve the very complex equations, the real situation has too many parameters and too many relations between them to succeed in having a full theoretical description of this phenomenon.

5 - Bibliography

Alonso, M., Finn, E.J., Fundamental University Physics, Addison Wesley, Reading, MA, 1967.
Anderson, H.L. ed., Physics Vademecum, Amer. Inst. of Physics, 1981.
Hoagland, A.S., Digital Magnetic Recording, Wiley, New York, 1963.
Jackson, J.D., Classical Electrodynamics, Wiley, New York, 1975.
Karlquist, O., Calculation of the Magnetic Field in Ferromagnetic Layer of a Magnetic Drum, Trans. Royal Inst. of Tech., Stockolm, 1954, vol.86,1.
Landau, L., Lifchiz E., Theorie des Champs, MIR, Moscou, 1970.
Milford, F.J., Reitz, J.R., Foundations of Electromagnetic Theory, Addison Wesley, Reading, MA, 1967.
Wallace, R.I. Jr., The Reproduction of Magnetically Recorded Signals, The Bell Tech. Journ., Oct. 1951.
IBM Journal of Research and Development, 1974, vol.18, n.6.
IBM, Disk Storage Technology, 1980.

(Figures 1.1, 2.2, 2.6, 3.2, 3.3, 3.4, 3.13 are from Hoagland, Digital Magnetic Recording)

Rodolfo Baggio, Introduction to Digital Magnetic Recording, IBM Customer Executives Briefing Center, Mainz, Germany, October, 1986